Guess-timating Integrals.

The 'Garden of Death' by Hugo Simberg. I find this piece to be really beautiful! I may do a write-up on it some day...

This is a neat tool I have picked up in the last couple of days that helps you guess/ascertain, at least partly, the form of an integral upon just a glance! Yes, no matter how complicated an integral might look, with this technique, you can sort of guess how the final form will look like, after just glancing the integral.

The only tool we need is dimensional analysis, something that is taught to every high-schooler.

To demonstrate the power of this tool, we'll do two examples to show it off - one where we guess-timate the form of the Gaussian integral and the other where we guess-timate a more general form of the Gamma Function!

THE GAUSSIAN INTEGRAL

Consider the form of the general Gaussian integral: $$ \int_{-\infty}^{\infty} e^{-\alpha x^2} dx $$

This integral is widely used everywhere (physics, statistics, pure mathematics, etc.) and no matter where it's used, the constant quantities are all stored in the $\alpha$ term and the variable quantity denoted by the $x$ term (I mean, that's how integrals work...).

So, notice that because this is being integrated w.r.t $x$ and because this is a definite integral, the $x$ term will not be present in the final form of the integral. We can reasonably guess that the $\alpha$ term will be there however. So, we can say that $$ \int_{-\infty}^{\infty} e^{-\alpha x^2} dx \qquad \propto \qquad f(\alpha) $$

Make no mistake, the $\propto$ symbol can mean 'proportional to' and also 'dimensionally equal to'. Now, also notice that the $-\alpha x^{2}$ is an exponent here. In general, exponents are just some quantity we raise another quantity by to tell us by how many times we should multiply the base by itself to get something else. So, what I'm saying is, this is a number, and numbers inherently don't have any dimensions themselves.

With this information, the dimensions of this exponent are: $$ [\alpha][x]^{2} = 1 $$

At this point, we first decide on a set of dimensions we ascribe so that the set itself is a perfectly consistent one and it doesn't break the 'dimensional validity' (more on this in a bit) of the integral. To be clear, we prescribe the variable in this expression (not the constant!), the dimension of our choice first. It doesn't matter if it is $[T]$ (time), $[M]$ (mass) or $[L]$ (length). Let's pick time $[T]$! So, $$ [x] = [T]$$ $$[\alpha] [x]^{2} = 1$$

Thus, $$[\alpha] = [T]^{-2}$$

Now, with this, we have that $[x] = [T]$. Two good thumb rules are that:

The differential operator, '$d$', doesn't affect the dimension of the term it is differentiating (or the term it is attached to, if you want a more pictorial wording).
The integral operator, '$\int$, doesn't affect dimensions of the integrand itself either!

With the first rule then, since $[x] = [T]$, $[dx] = [T]$ too, so to speak. And then, by the second rule, the integral itself boils down to (dimensionally speaking): $$ \int_{-\infty}^{\infty} e^{-\alpha x^2} dx = [T] $$

So now, we know that the integral will be equal to a quantity whose dimension is just $[T]$. Now, what known/persistent quantity do we know that has a dimension of $[T]$? That's right! It's our constant term, $\alpha$. This is what I meant earlier by choosing a set of dimensions that will preserve 'dimensional validity' of the integral.

Now, how do we go from this: $$[\alpha] = [T]$$ to this: $$[T]^{-2}$$

That's simple, just take the inverse of the square root of $\alpha$! And lo and behold, we come to an approximation of the general Gaussian integral $$ \int_{-\infty}^{\infty} e^{-\alpha x^2} dx \approx \dfrac{1}{\sqrt{\alpha}} $$

Upon checking the actual answer, you can see that what we're missing is just the $\sqrt{\pi}$ in the numerator! The reason why this didn't pop up is again, because our dimensional analysis only picks up on quantities that have dimensions inherent to them. But nonetheless, this is a pretty good 'at-a-glance' estimate!

A GENERAL GAMMA FUNCTION

In a more quick-paced manner, I have provided below my working for how we can approximate the final form (or at least a component) of the generalized Gamma function's integral: $$ I(k) = \int_{0}^{\infty} t^{z-1} e^{-kt} dt $$

The solution:

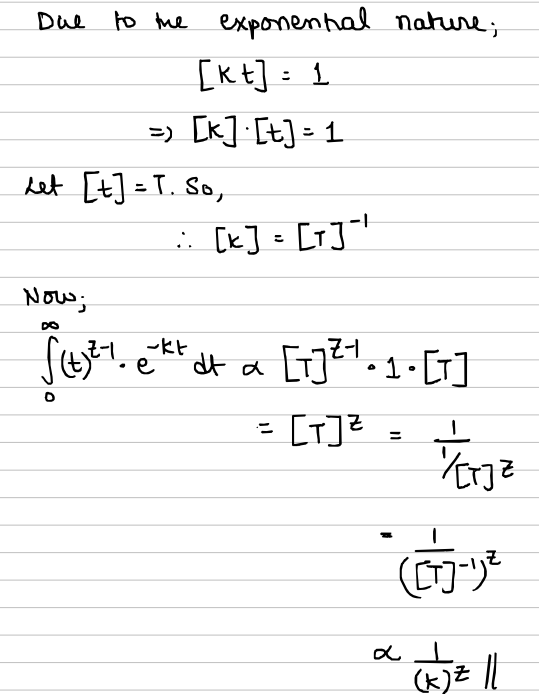
Some good exercises to apply this technique in:

A) Other integrals, definite or not, where they result in known (or unknown) trigonometric forms!

B) To redo the same guess-timating without dimensional analysis! Try this for the Gaussian integral first, as that might give you some insight into how this pathway works...

C) Integrals (again, definite or not) where there are no exponential quantities. Maybe polynomial terms in the denominator (where you might once apply partial fractions) or other forms too, just without the limitation of having exponents!

And that's it! That's how you can guess-timate integrals using dimensional analysis as a tool. I hope you enjoyed this short article, as it was my first forray into writing about problem-solving techniques that I find pretty cool!